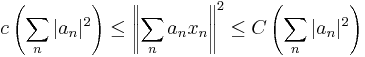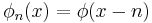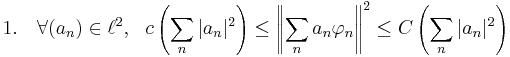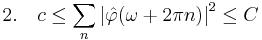Riesz sequence
In mathematics, a sequence of vectors (xn) in a Hilbert space 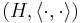 is called a Riesz sequence if there exist constants
is called a Riesz sequence if there exist constants 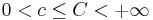 such that
such that
for all sequences of scalars (an) in the ℓp space ℓ2. A Riesz sequence is called a Riesz basis if
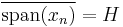 .
.
Theorems
If H is a finite-dimensional space, then every basis of H is a Riesz basis.
Let φ be in the Lp space L2(R), let
and let 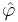 denote the Fourier transform of φ. Define constants c and C with
denote the Fourier transform of φ. Define constants c and C with 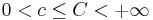 . Then the following are equivalent:
. Then the following are equivalent:
The first of the above conditions is the definition for (φn) to form a Riesz basis for the space it spans.
See also
This article incorporates material from Riesz sequence on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.
This article incorporates material from Riesz basis on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.